Transformación afín

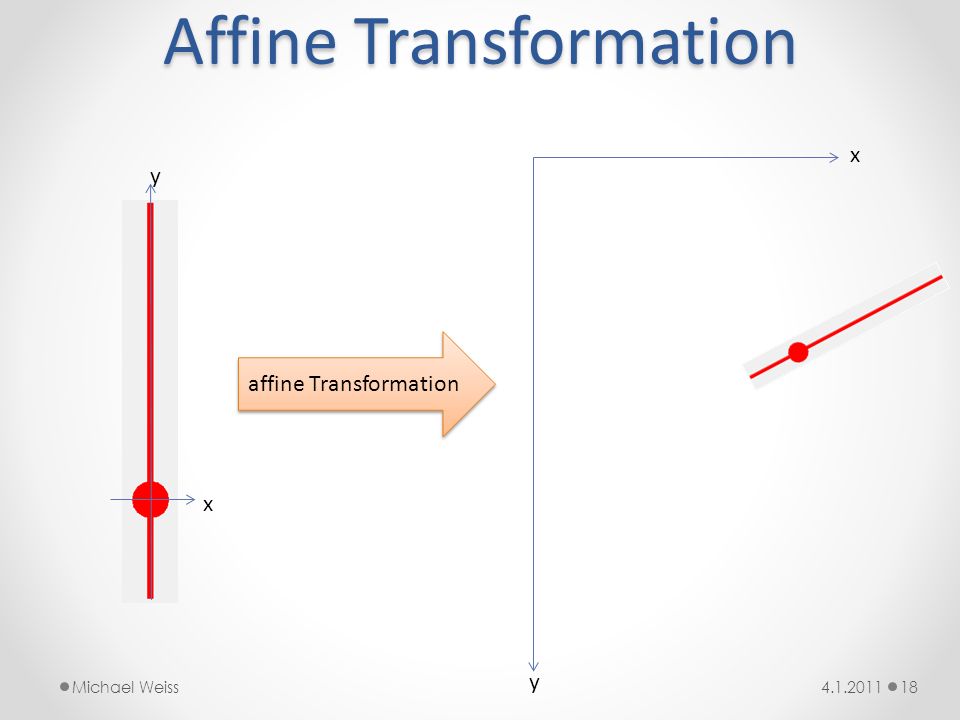
En geometría, una transformación afín o aplicación afín (también llamada afinidad) entre dos espacios afines (en particular, dos espacios vectoriales) consiste en una transformación lineal seguida de una traslación:

${\displaystyle \mathbf {x} \mapsto \mathbf {A} \mathbf {x} \mathbf {b} }$

En el caso de dimensión finita, toda transformación afín puede representarse por una matriz ${\displaystyle \mathbf {A} }$ y un vector ${\displaystyle \mathbf {b} }$ que satisfacen ciertas propiedades que se especifican más adelante.

Geométricamente, una transformación afín en un espacio euclídeo es una transformación que preserva:

1. Las relaciones de colinealidad (y coplanaridad) entre puntos, es decir, puntos que recaían sobre una misma línea (o sobre un mismo plano) antes de la transformación, son preservadas tras una transformación afín.
2. Las razones entre distancias a lo largo de una línea, es decir, para tres puntos alineados distintos ${\displaystyle P_{1},P_{2},P_{3},}$ las razones ${\displaystyle |{\overline {P_{2}P_{1}}}|/|{\overline {P_{3}P_{2}}}|}$ antes y después de la transformación son iguales.

En general, una transformación afín está compuesta de transformaciones lineales (rotaciones, homotecias y cizallamientos) compuestas con una traslación o desplazamiento. En el caso 1-dimensional A y b se llaman, respectivamente, la pendiente y el término independiente.

Definición matemática

Una transformación afín ${\displaystyle f:\mathbb {A} \rightarrow \mathbb {A} '}$ entre dos espacios afines ${\displaystyle (\mathbb {A} ,E,\delta )}$ y ${\displaystyle (\mathbb {A} ',E',\delta ')}$es una aplicación sobre los puntos que actúa linealmente sobre los vectores que los unen. Formalmente, ${\displaystyle f}$ es una transformación afín si existe una aplicación lineal ${\displaystyle g}$ tal que ${\displaystyle \forall p,q\in \mathbb {A} ,}$

${\displaystyle {\overrightarrow {f(p)~f(q)}}=g({\overrightarrow {pq}})}$.

Propiedades

Caracterización geométrica

Veremos ahora que las transformaciones afines son y sólo son aquellas que conservan alineaciones de puntos y razones simples. Para ello, primero vamos a definir formalmente estas condiciones:

Dada ${\displaystyle f:\mathbb {A} \rightarrow \mathbb {A} '}$, diremos que ${\displaystyle f}$ conserva alineaciones de puntos si

${\displaystyle m\in \left\langle p,q\right\rangle \Rightarrow f(m)\in \langle f(p),f(q)\rangle \quad \forall p,q,m\in \mathbb {A} }$,

donde ${\displaystyle \langle S\rangle }$ representa el conjunto de las combinaciones afines del conjunto ${\displaystyle S}$ o lo que es lo mismo, la variedad lineal más pequeña que contiene a ${\displaystyle S}$. La demostración de esto último se puede ver en el artículo de combinaciones afines.

Además, diremos que ${\displaystyle f}$ conserva razones simples si cumple dos condiciones:

• ${\displaystyle f}$ conserva razones de puntos
• Si ${\displaystyle p,q,m\in \mathbb {A} }$ están alineados y ${\displaystyle f(p)\neq f(q)}$ entonces ${\displaystyle (p,q,m)=\left(f(p),f(q),f(m)\right)}$,

donde, dados ${\displaystyle a,b,c\in \mathbb {A} }$ alineados tales que ${\displaystyle a\neq b}$, definimos la razón simple ${\displaystyle (a,b,c)=\lambda \in \mathbb {K} }$ si ${\displaystyle {\overrightarrow {ac}}=\lambda \cdot {\overrightarrow {ab}}}$ .

Con estas definiciones, tenemos el siguiente teorema:

Representación

El álgebra vectorial ordinaria usa la multiplicación por matrices para representar transformaciones lineales y la suma de vectores para representar traslaciones. Mediante "matrices ampliadas", resulta posible representar ambos tipos de transformaciones exclusivamente mediante multiplicación por matrices. La técnica para "ampliar los vectores" consiste en añadir un vector con una componente extra de valor unitario al resto de las componentes y a todas las matrices se le añade una columna al final con el vector que da la traslación y una fila al final con componentes cero y un 1 en la última posición, es decir:

${\displaystyle {\begin{pmatrix}x'_{1}\\\vdots \\x'_{n}\end{pmatrix}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &\ddots &\vdots \\a_{n1}&\dots &a_{nn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}} {\begin{pmatrix}b_{1}\\\vdots \\b_{n}\end{pmatrix}}\,\,\sim \,\,{\begin{pmatrix}x'_{1}\\\vdots \\x'_{n}\\1\end{pmatrix}}={\begin{pmatrix}a_{11}&\dots &a_{1n}&b_{1}\\\vdots &\ddots &\vdots &\vdots \\a_{n1}&\dots &a_{nn}&b_{n}\\0&\dots &0&1\end{pmatrix}}{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\\1\end{pmatrix}}}$

O en forma más compacta:

${\displaystyle {\vec {y}}=\mathbf {A} {\vec {x}} {\vec {b}}\,\,\sim \,\,{\begin{pmatrix}{\vec {y}}\\1\end{pmatrix}}={\begin{pmatrix}\mathbf {A} &{\vec {b}}\ \\0,\ldots ,0&1\end{pmatrix}}{\begin{pmatrix}{\vec {x}}\\1\end{pmatrix}}}$

Esta representación permite ver rápidamente que el conjunto de todas las transformaciones afines invertibles es el producto semidirecto ${\displaystyle \mathbb {K} ^{n}\oplus {\text{GL}}(n,\mathbb {K} )}$; el grupo anterior bajo la operación de composición de transformaciones es un grupo llamado grupo afín de orden n. Como puede verse este grupo es un subgrupo de ${\displaystyle {\text{GL}}(n 1,\mathbb {K} )}$.

Isometrías y semejanzas

Una transformación es invertible si y sólo si ${\displaystyle \mathbf {A} }$ es invertible. En la representación matricial descrita anteriormente, la inversa tiene la forma:

${\displaystyle {\begin{bmatrix}\mathbf {A} ^{-1}&-\mathbf {A} ^{-1}{\vec {b}}\ \\0,\ldots ,0&1\end{bmatrix}}}$

Las transformaciones afines invertibles (de un espacio afín en sí mismo) forman el llamado grupo afín que como se ha mencionado tiene al grupo lineal de orden n como subgrupo. El propio grupo afín de orden n es a su vez subgrupo del grupo lineal de orden n 1.

Transformación de imágenes

En el ámbito del procesamiento digital de imágenes, las transformaciones afines son análogas a imprimir en una hoja de goma y estirar los bordes de forma paralela al plano. Esta transformación reubica los píxeles que requieren interpolación de intensidad para aproximar el valor de los píxeles desplazados; la interpolación bicúbica es el estándar para hacer las transformaciones de imágenes en las aplicaciones de procesamiento de la imagen. Las transformaciones afines escalar, rotan, y hacen simetría especular y cizallamiento de imágenes según los ejemplos siguientes:

Referencias

Bibliografía

• Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3 .
• Nomizu, Katsumi; Sasaki, S. (1994), Affine Differential Geometry (New edición), Cambridge University Press, ISBN 978-0-521-44177-3 .
• Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. Nueva York: Springer. ISBN 0-387-94732-9.